Sympyとは
科学技術計算ライブラリ
Sympyは数学や科学、工学などの分野で広く使用されており、数式処理を行うための強力なPythonライブラリです。Sympyを使用すると、以下のような数学的な問題を解決することができます。
- 方程式の解
- 連立方程式の解
- 式展開
- 式を因数分解
- 微分・積分計算
- 行列の計算
Sympyの特徴
Sympyには以下のような特徴があります。
シンボリック計算
シンボリック計算とは、式の展開、因数分解、微分、積分などの数学的などを数式を数値ではなく文字列記号として扱う操作のことです。 Sympyはシンボリック計算で処理するPythonライブラリです。
便利な関数
微分、積分、方程式の解法など、様々な数学的な関数が用意されています。
ユーザー定義の記号
ユーザー独自の記号を定義することができます。
LaTeXとの連携
Sympyの出力をLaTeXの形式で取得することができ、数式を美しく表示できます。
Sympyのインストール
Sympyはpipを使ってインストールできます。
- Condaでインストール済みの場合は必要ありません
pip install sympy
Sympyの基本的な使い方
モジュールインポート
Sympyを使用するには、まずSympyモジュールをインポートします。
from sympy import *
モジュールを部分的に読み込むこともできます。
from sympy import symbols, Eq, solve
シンボル定義
計算式のためのシンボルを symbols() を使って定義します。 「x」「y」「z」という3つのシンボルを定義します。
x, y, z = symbols('x y z')
数式の作成
シンボルを使って数式を作成することができます。例えば、以下の数式を定義します。
$$ (x + y)^2 $$
expr = (x + y)**2
# (x + y)**2
数式の作成
expand() で数式を変形することができます。
$$ x^2 + 2xy + y^2 $$
expanded = expand((x + y)**2)
# x**2 + 2*x*y + y**2
1次方程式
次の1次方程式のグラフと交点座標を求めます。
$$ y = 2x + 1 $$ $$ y = -x + 4 $$
基本設定
インポート
Sympy、Matplotlib、Numpyをインポートします。
sympy_sample_1.py
from sympy import *
import matplotlib.pyplot as plt
import numpy as np
シンボル定義
symbols() で数式のシンボルを定義します。
sympy_sample_1.py
from sympy import *
import matplotlib.pyplot as plt
import numpy as np
# シンボルの定義
x, y = symbols('x y')
方程式の定義
シンボルと係数を利用して、1次方程式をそれぞれ定義します。
sympy_sample_1.py
from sympy import *
import matplotlib.pyplot as plt
import numpy as np
x, y = symbols('x y')
# 係数の定義
a1 = 2
b1 = 1
a2 = -1
b2 = 4
# 方程式の定義
eq1 = y - a1*x - b1
eq2 = y - a2*x - b2
方程式の解
solve() で連立1次方程式を解きます。
sympy_sample_1.py
from sympy import *
import matplotlib.pyplot as plt
import numpy as np
x, y = symbols('x y')
a1 = 2
b1 = 1
a2 = -1
b2 = 4
eq1 = y - a1*x - b1
eq2 = y - a2*x - b2
# 連立方程式の解
result = solve((eq1, eq2))
print(result)
交点 x、y の値が求まりました。
$$ (x, y) = (1, 3) $$
結果
{x: 1, y: 3}
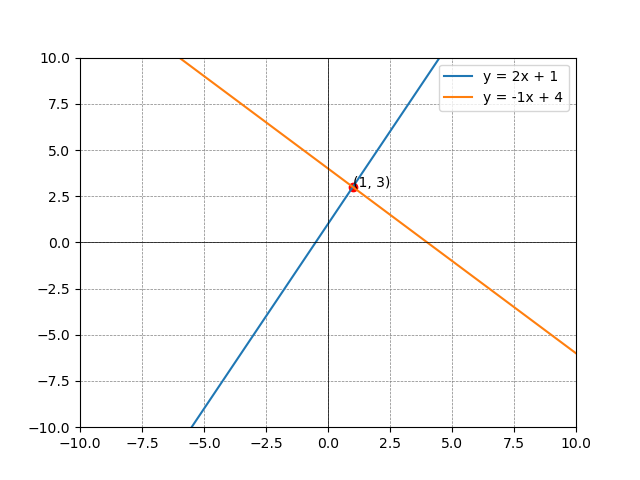
グラフ作成
$$ y = 2x + 1 $$ $$ y = -x + 4 $$
のグラフを描画し、求めた交点座標もプロットします。

sympy_sample_1.py
from sympy import *
import matplotlib.pyplot as plt
import numpy as np
# シンボルの定義
x, y = symbols('x y')
# 係数の定義
a1 = 2
b1 = 1
a2 = -1
b2 = 4
# 方程式の定義
eq1 = y - a1*x - b1
eq2 = y - a2*x - b2
# 連立方程式の解
result = solve((eq1, eq2))
print(result)
# グラフプロット
x_data = np.linspace(-10, 10, 100)
y1_data = a1*x_data + b1
y2_data = a2*x_data + b2
# グラフ描画
plt.plot(x_data, y1_data, label=f"y = {a1}x + {b1}")
plt.plot(x_data, y2_data, label=f"y = {a2}x + {b2}")
plt.scatter(result[x], result[y], color="red")
label = f"({result[x]}, {result[y]})"
plt.annotate(label, (result[x], result[y]))
plt.xlim(-10, 10)
plt.ylim(-10, 10)
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.legend()
plt.grid(color='gray', linestyle='--', linewidth=0.5)
plt.show()
2次方程式
解の公式
2次方程式の解の公式は以下の通りです。
$$ y =ax^2+bx + c $$ $$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
Sympyでは solve() を利用して、x を求められます。
result = solve(y, x)
2次方程式を解く
数式作成
係数を $$ a = 1, b = 2, c = -1 $$
として、
$$ y = x^2+2x -1 $$
の数式を作成します。
sympy_sample_2.py
from sympy import *
import matplotlib.pyplot as plt
import numpy as np
# 数式作成
a, b, c = 1, 2, -1
x, y = symbols('x, y')
y = a*x**2 + b*x + c
解を求める
solve() で、x を求めてみます。
sympy_sample_2.py
from sympy import *
import matplotlib.pyplot as plt
import numpy as np
a, b, c = 1, 2, -1
x, y = symbols('x, y')
y = a*x**2 + b*x + c
# 解を求める
result = solve(y, x)
print(result)
解は以下のようになりました。
$$ x = -1 \pm \sqrt{2} $$
結果
[-1 + sqrt(2), -sqrt(2) - 1]
グラフ作成
プロットデータ作成
y は x のデータを繰り返して、方程式の計算をします。
$$ y = x^2+ 2x + -1 $$
# グラフプロット
x_data = np.arange(-10, 10, 0.1)
y_data = [y.subs(Symbol('x'), value) for value in x_data]
plt.plot(x_data, y_data)
- x は「-10」から「10」で「0.1」ステップのデータを作成します。
解のプロット
解 x の座標を scatter() でプロットします。
$$ x = -1 \pm \sqrt{2} $$
# 解のプロット
for value in result:
plt.scatter(value, 0)
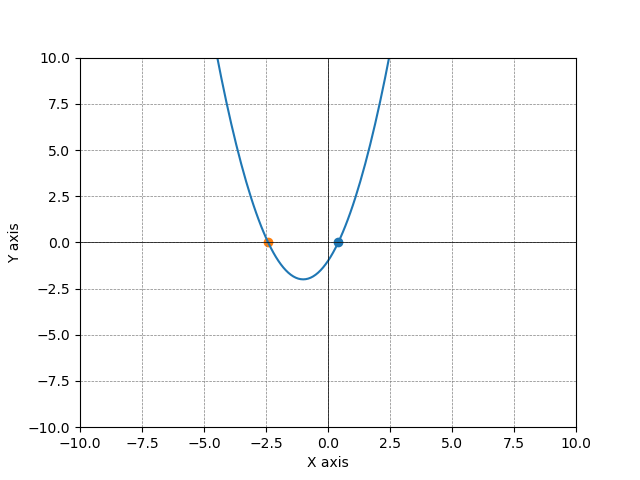
グラフ描画
これらデータをグラフ描画します。
from sympy import *
import matplotlib.pyplot as plt
import numpy as np
# 数式作成
x = symbols('x')
a, b, c = 1, 2, -1
y = a*x**2 + b*x + c
# 解
result = solve(y, x)
print(result)
# グラフプロット
x_data = np.arange(-10, 10, 0.1)
y_data = [y.subs(x, value) for value in x_data]
plt.plot(x_data, y_data)
# 解のプロット
for value in result:
plt.scatter(value, 0)
plt.xlim(-10, 10)
plt.ylim(-10, 10)
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.xlabel('X axis')
plt.ylabel('Y axis')
plt.grid(color = 'gray', linestyle = '--', linewidth = 0.5)
plt.show()
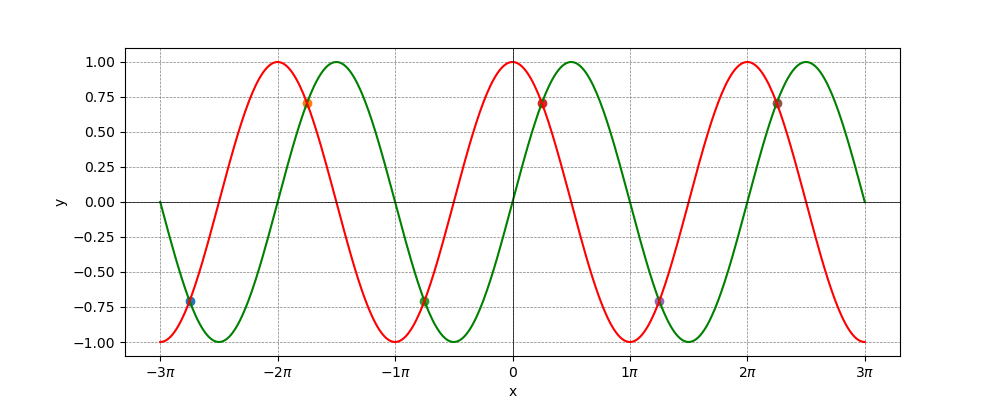
三角関数
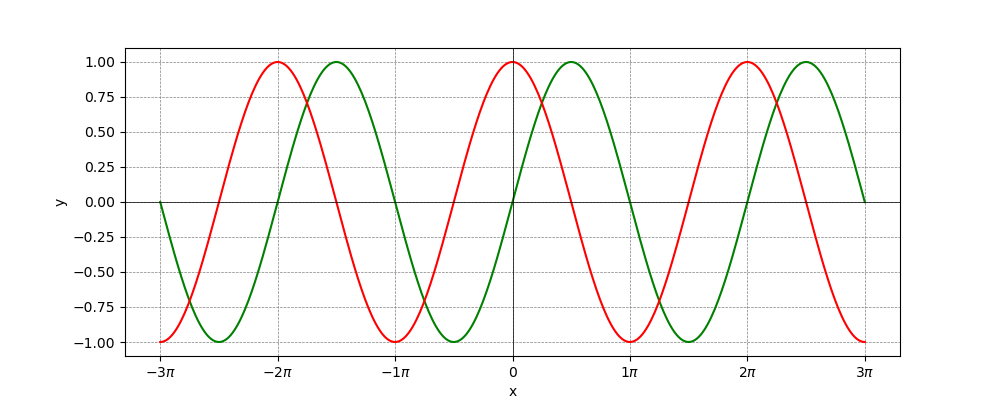
以下の三角関数(sin, cos)のグラフとその交点をグラフにします。
$$ y = a_1 sin(x) + b_1$$ $$ y = a_2 cos(x) + b_2 $$ $$ 3\pi \leq x \leq 3\pi$$
グラフ表示
データ生成
-3πから3πまでのXデータを生成します。 Yデータはそれぞれ sin(x)、cos(x) とします。
sympy_sample_3
# x値の範囲を生成 (-3π から 3πまで)
min = -np.pi*3
max = np.pi*3
# 係数設定
a1 = 2
a2 = 1
b1 = 0
b2 = 0
#### データ生成
Xデータと、対応するYデータを *sin(x)*、*cos(x)* で生成します。
###### sympy_sample_3
```python
# xを400サンプル生成
x_data = np.linspace(min, max, 400)
# yデータ生成
y1_data = np.sin(x_data)
y2_data = np.cos(x_data)
グラフ表示
生成したデータをグラフ表示します。
sympy_sample_3
# グラフサイズ
plt.figure(figsize=(10, 4))
# グラフをプロット
plt.plot(x_data, y1_data, color="green")
plt.plot(x_data, y2_data, color="red")
# タイトルと軸ラベルを追加
plt.xlabel('x')
plt.ylabel('y')
# 目盛り
x_ticks = np.arange(min, max + np.pi, np.pi)
x_tick_labels = [f"${s:.0f}\\pi$" if s != 0 else '0' for s in x_ticks / np.pi]
# グリッドを表示
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.grid(color = 'gray', linestyle = '--', linewidth = 0.5)
plt.show()
交点の座標を求める
解を求める
範囲指定して、solveset() で複数の解を求めます。
eq = sin(x) - cos(x)
results = solveset(eq, x, domain=Interval(min, max))
print(results)
結果
{-11*pi/4, -7*pi/4, -3*pi/4, pi/4, 5*pi/4, 9*pi/4}
解のプロット
複数の解から交点をプロットします。
# 解のプロット
for result in results:
x_plot = result
y_plot = a1 * sin(x_plot) + b1
plt.scatter(x_plot, y_plot)

演習
問題1
以下のグラフになるように、a1,a2,b1,a2 をそれぞれ設定してみましょう。
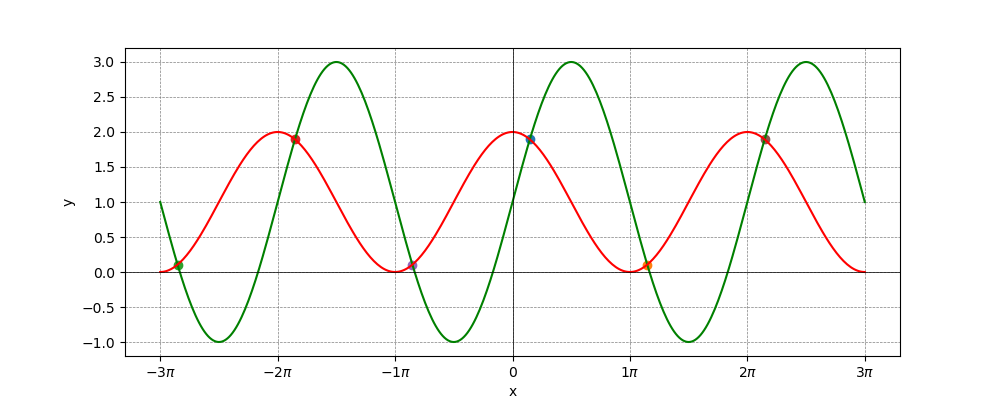
問題2
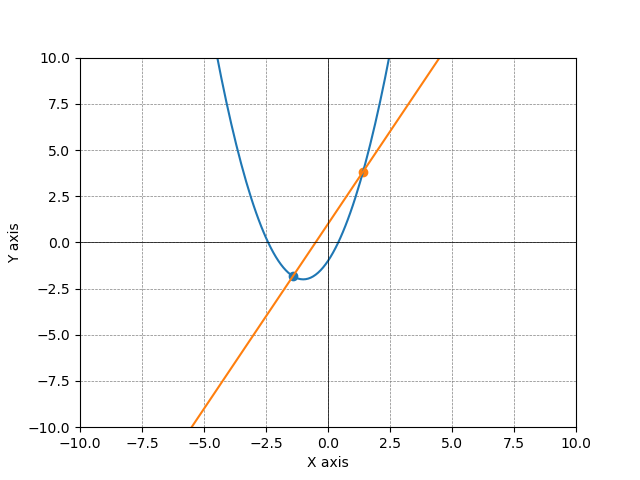
以下の式と交点をグラフ表示してみましょう。
$$ y = x^2+2x -1 $$ $$ y = 2x+1 $$