Matplotlibとは
グラフ描画ライブラリ
MatplotlibはPythonのグラフ描画ライブラリで、データの視覚化に広く使用されています。 線グラフ、散布図、ヒストグラム、バークラフ、エラーバー、箱ひげ図、ヒートマップなど、様々なタイプのグラフを簡単に作成できます。
Matplotlibの利用方法
Matplotlibのインストール
Matplotlibを使用するには、pipインストールが必要です。
- Anacondaを利用している場合、すでにインストールされています
ターミナル
pip install matplotlib
インポート
Matplotlibを使用するには、matplotlib.pyplotモジュールをインポートします。pyplotは、Matplotlibを使ってグラフを簡単に描画できます。
import matplotlib.pyplot as plt
主な関数
Matplotlibは、データを視覚化するための様々な関数が搭載されています。
基本的な描画関数
show()
グラフを表示します。
show()
plot()
複数のX, Yデータセットを渡して線グラフやマーカーをプロットします。線やマーカーのスタイルをカスタマイズできます。
plot(x, y)
scatter()
散布図を描画します。サイズや色をデータポイントなどををカスタマイズできます。
scatter(x, y, ...)
bar()
水平の棒グラフを描画します。棒の高さや幅、色などをカスタマイズできます。
bar(x, y, ...)
barh()
垂直の棒グラフを描画します。
barh(x, y, ...)
hist()
ヒストグラムを描画します。データの分布を可視化するのに便利です。
hist(x, ...)
軸とグリッドの設定
title()
グラフにタイトルを設定します。
title(タイトル文字, ...)
xlabel()/ylabel()
X軸やY軸のタイトル(ラベル)を設定します。
xlabel(X軸タイトル, ...)
ylabel(Y軸タイトル, ...)
xlim()/ylim()
X軸やY軸の表示範囲を設定します。
xlim(left, right, ...)
ylim(left, right, ...)
xticks()/yticks()
X軸やY軸の目盛りの位置やラベルを設定します。
xticks(positions, labels, ...)
yticks(positions, labels, ...)
grid()
グラフにグリッド線を追加します。表示のオンオフやスタイルのカスタマイズできます。
grid(color = "色", linestyle = "スタイル", linewidth = 幅, ...)
axhline()/axvline()
垂直、水平線を描画します。
axhline(Y座標, color = "色", linestyle = "スタイル", linewidth = 幅, ...)
axvline(X座標, color = "色", linestyle = "スタイル", linewidth = 幅, ...)
その他
figure()
新しいフィギュア(描画領域)を作成したり、図のサイズや解像度を設定できます。
figure(フィギュア番号を指定, figsize=(x, x), ...)
subplot()
サブプロットを作成します。1つのウィンドウ内に複数のグラフを配置できます。
subplot(行数, 列数, サブプロット番号)
legend()
凡例を追加します。データセットのラベルを説明するのに役立ちます。
legend()
線グラフ
線グラフの基本
X座標, Y座標のリストを作成し、plot() で線グラフ、scatter() で座標マーカーを表示します。

インポート
matplotlib.pyplot をインポートします。
graph_sample_1.py
import matplotlib.pyplot as plt
線グラフ表示
X, Yデータを生成し、線グラフ表示します。
graph_sample_1.py
import matplotlib.pyplot as plt
x = [-3, -1, 2, 4]
y = [-2, 1, 3, 2]
# データプロット
plt.plot(x, y)
plt.show()
結果

座標表示
scatter() で、X, Y座標を表示をします。
graph_sample_1.py
import matplotlib.pyplot as plt
x = [-3, -1, 2, 4]
y = [-2, 1, 3, 2]
plt.plot(x, y)
# 散布図プロット
plt.scatter(x, y)
plt.show()

グラフのカスタマイズ
軸設定やグリッドなどを調整します。
graph_sample_1.py
import matplotlib.pyplot as plt
x = [-3, -1, 2, 4]
y = [-2, 1, 3, 2]
# プロット
plt.plot(x, y)
plt.scatter(x, y)
# X, Y軸ラベル
plt.xlabel('X')
plt.ylabel('Y')
# 軸範囲
plt.xlim(-10, 10)
plt.ylim(-10, 10)
# 目盛り
plt.xticks(range(-10, 11, 2))
plt.yticks(range(-10, 11, 2))
# ゼロ線
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
# グリッド線
plt.grid(color = 'gray', linestyle = '--', linewidth = 0.5)
# グラフ描画
plt.show()
結果

円グラフ
pie()
pie() で円グラフを描画します。カテゴリー別の割合を視覚化します。
pie(sizes, labels, ...)
円グラフの例
ラベルとリストデータを用意し、pie() で円グラフを描画します。
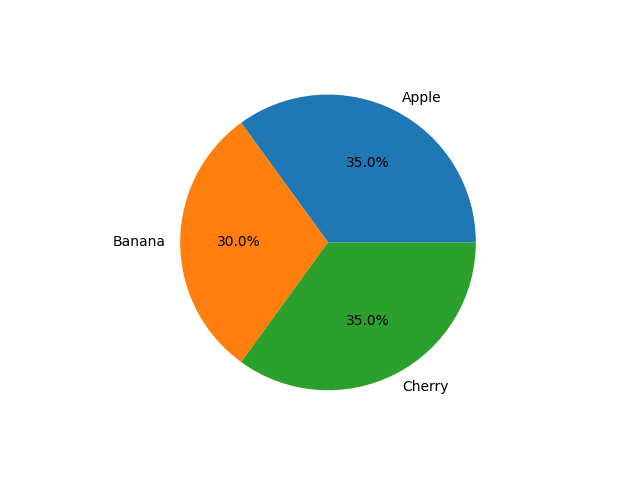
graph_sample_2.py
import matplotlib.pyplot as plt
labels = 'Apple', 'Banana', 'Cherry'
sizes = [35, 30, 35]
plt.pie(sizes, labels=labels, autopct='%1.1f%%')
plt.show()
ベクトル図
quiver()
quiver() はベクトル場を可視化する関数で、2次元や3次元のベクトル表示します。
quiver(X, Y, U, V)
ベクトル図の例

始点座標とベクトル(移動距離)を指定してベクトル表示します。
graph_sample_3.py
import matplotlib.pyplot as plt
# 始点
x1, y1 = 0, 0
# ベクトル
v1, w1 = 4, 2
v2, w2 = 2, 2
plt.quiver(x1, y1, v1, w1, color='red', angles='xy', scale_units='xy', scale=1)
plt.quiver(v1, w1, v2, w2, color='green', angles='xy', scale_units='xy', scale=1)
plt.xlim([0,10])
plt.ylim([0,10])
plt.grid()
plt.show()
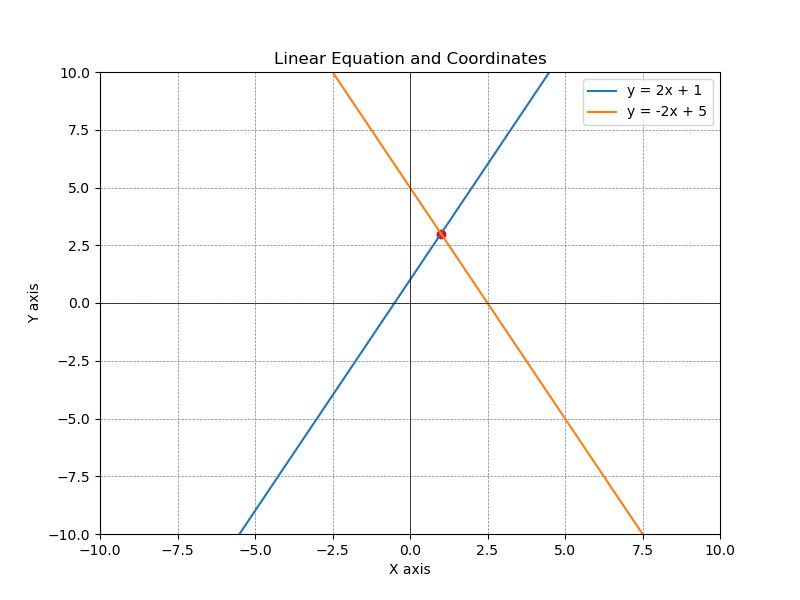
一次方程式のグラフ
$$ y = 2x + 1 $$ $$ y = -2x + 5 $$
の一次方程式をグラフで表示します。
ライブラリインポート
必要なライブラリをインポートします。
graph_sample_4.py
import numpy as np
import matplotlib.pyplot as plt
X軸データ作成
「-10」から「10」までの「100」個の連続データ(X軸)を、Numpyのlinspace() で作成します。
graph_sample_4.py
# xの連続データ
x = np.linspace(-10, 10, 100)
print(x)
結果
[-10. -9.7979798 -9.5959596 -9.39393939 -9.19191919
-8.98989899 -8.78787879 -8.58585859 -8.38383838 -8.18181818
...
Y軸データ作成
2つの1次方程式の係数から、Y軸のデータを作成します。
graph_sample_4.py
# 係数
a1, a2 = 2, -2
b1, b2 = 1, 5
# Yの連続データ
y1 = a1 * x + b1
y2 = a2 * x + b2
print(y1)
print(y2)
結果
[-1.90000000e+01 -1.85959596e+01 -1.81919192e+01 -1.77878788e+01
-1.73838384e+01 -1.69797980e+01 -1.65757576e+01 -1.61717172e+01
...
[ 25. 24.5959596 24.19191919 23.78787879 23.38383838
22.97979798 22.57575758 22.17171717 21.76767677 21.36363636
...
グラフ表示
2つの1次方程式を線グラフで表示します。
graph_sample_4.py
# グラフ表示
plt.plot(x, y1, label=f"y = {a1}x + {b1}")
plt.plot(x, y2, label=f"y = {a2}x + {b2}")
# 軸範囲
plt.xlim(-10, 10)
plt.ylim(-10, 10)
# ゼロ線
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
# 軸ラベル
plt.xlabel('X axis')
plt.ylabel('Y axis')
# 判例
plt.legend()
# グリッド線
plt.grid(color = 'gray', linestyle = '--', linewidth = 0.5)
plt.show()
結果
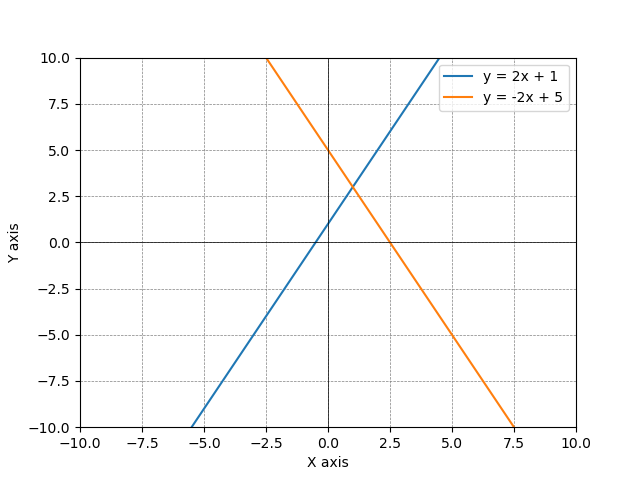
解の表示
2つの1次方程式の解を線形代数で計算します。 解を計算するためには、
式の変形
各1次方程式が「0」になるように変形します。
$$ a_1 x - y + b_1= 0 $$ $$ a_2 x - y + b_2= 0 $$
これら式から、係数の行列と定数ベクトルを定義します。
係数の行列
$$ A = \begin{bmatrix} a_1 & -1\\ a_2 & -1 \end{bmatrix} $$
定数ベクトル
$$ b = \begin{bmatrix} b_1 & b_2 \end{bmatrix} $$
係数の行列と定数ベクトルを定義します。
graph_sample_4.py
# 係数
a1, a2 = 2, -2
b1, b2 = 1, 5
...
# 係数行列
A = np.array([[a1, -1], [a2, -1]])
# 定数ベクトル
b = np.array([-b1, -b2])
print(A)
print(b)
結果
[[ 2 -1]
[-2 -1]]
[-1 -5]
方程式の解の計算
方程式の解は、Numpyの solve() で計算できます。
graph_sample_4.py
# 方程式の解
point = np.linalg.solve(A, b)
print("(x, y)", point[0], point[1])
「x = 1」「y = 3」となりました。
結果
(x, y) 1.0 3.0
解のプロット
解を scatter() でプロットした全体のプログラムです。

graph_sample_4.py
import numpy as np
import matplotlib.pyplot as plt
# 係数
a1, a2 = 2, -2
b1, b2 = 1, 5
# xの連続データ
x = np.linspace(-10, 10, 100)
print(x)
# Yの連続データ
y1 = a1 * x + b1
y2 = a2 * x + b2
print(y1)
print(y2)
# グラフ表示
plt.plot(x, y1, label=f"y = {a1}x + {b1}")
plt.plot(x, y2, label=f"y = {a2}x + {b2}")
# 係数行列
A = np.array([[a1, -1], [a2, -1]])
# 定数ベクトル
b = np.array([-b1, -b2])
print(A)
print(b)
# 方程式の解
point = np.linalg.solve(A, b)
print("(x, y)", point[0], point[1])
# 解のプロット
plt.scatter(point[0], point[1], color='red')
plt.xlim(-10, 10)
plt.ylim(-10, 10)
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.xlabel('X axis')
plt.ylabel('Y axis')
plt.legend()
plt.grid(color = 'gray', linestyle = '--', linewidth = 0.5)
plt.show()
